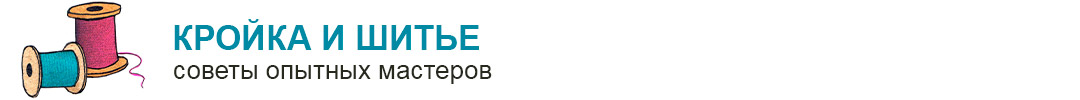Какой формулой в конусе можно связать длину образующей l высоту h и радиус r
Обновлено: 01.05.2024
Каждый школьник слышал о круглом конусе и представляет, как выглядит эта объемная фигура. В данной статье дается определение развертки конуса, приводятся формулы, описывающие ее характеристики, а также описывается способ ее построения с помощью циркуля, транспортира и линейки.
Круглый конус в геометрии
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Вам будет интересно: Юридический колледж в Иваново: специальности, приемная комиссия, отзывы
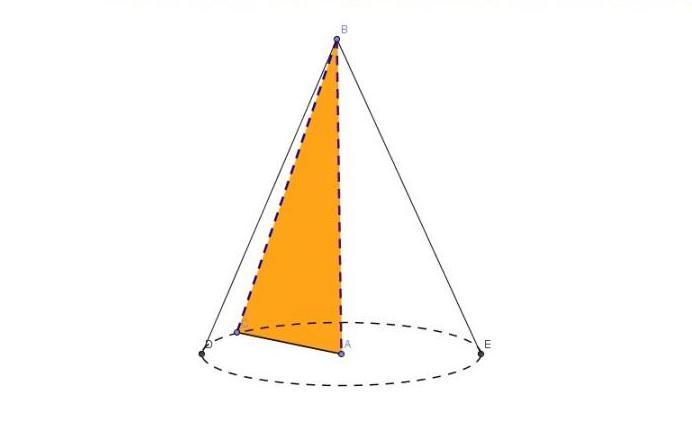
Круг называется основанием фигуры, его окружность - это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются - это вершина конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.
Вам будет интересно: Термофильные бактерии: польза и вред для человека
Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Получение фигуры с помощью вращения
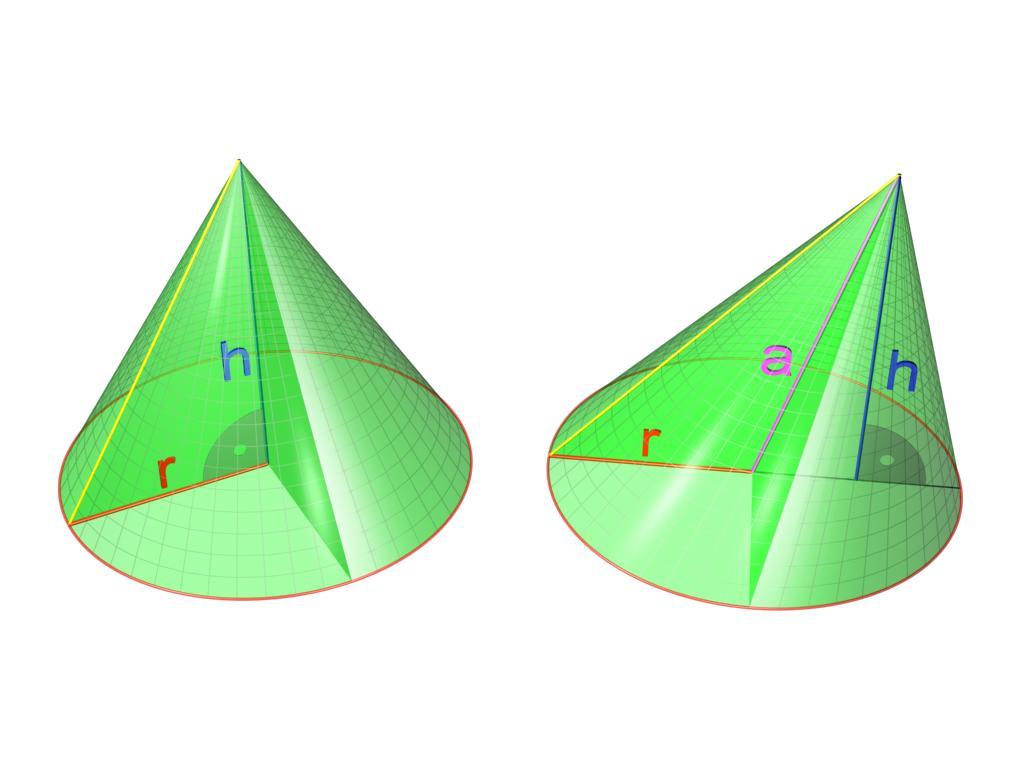
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
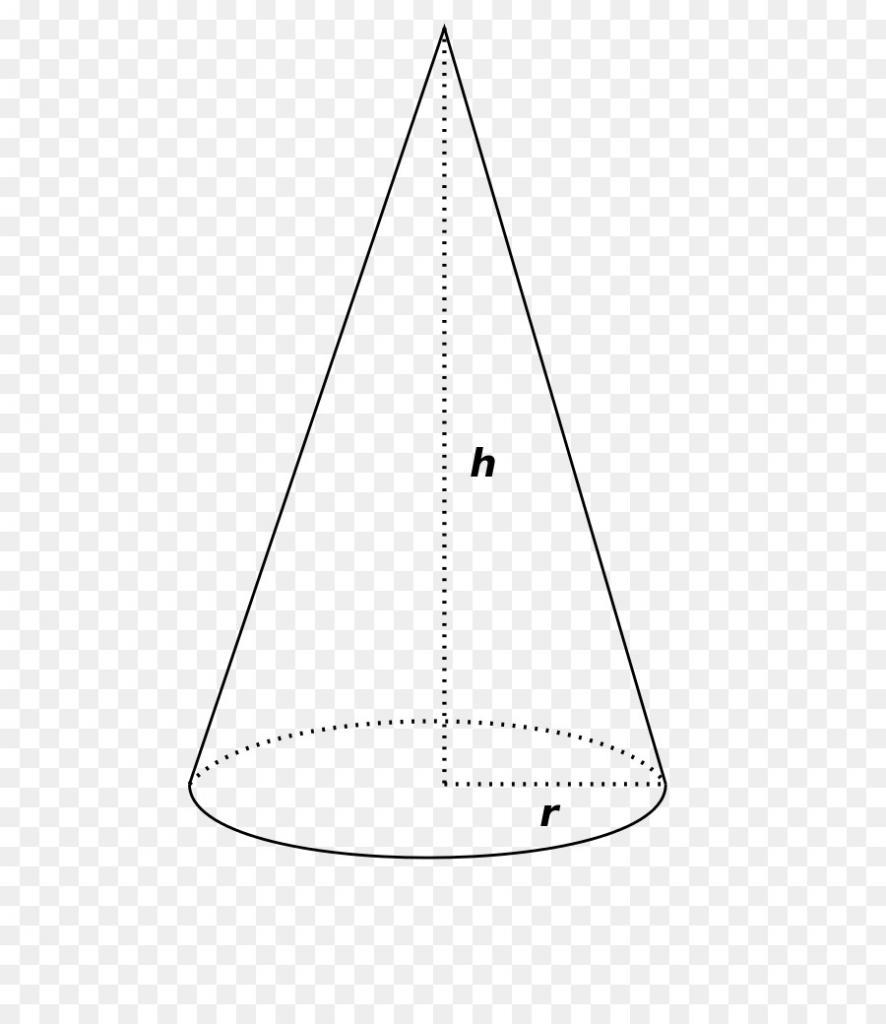
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c - это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Очевидно, что катет a будет радиусом основания фигуры, катет b - его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Вид развертки конуса
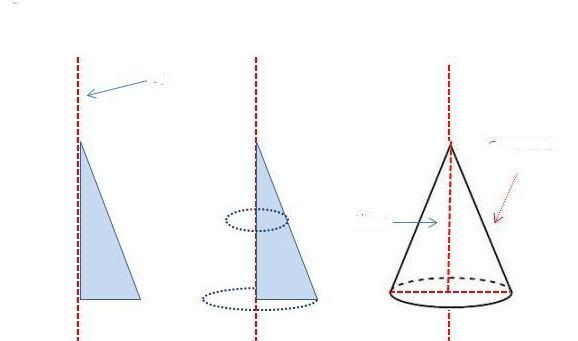
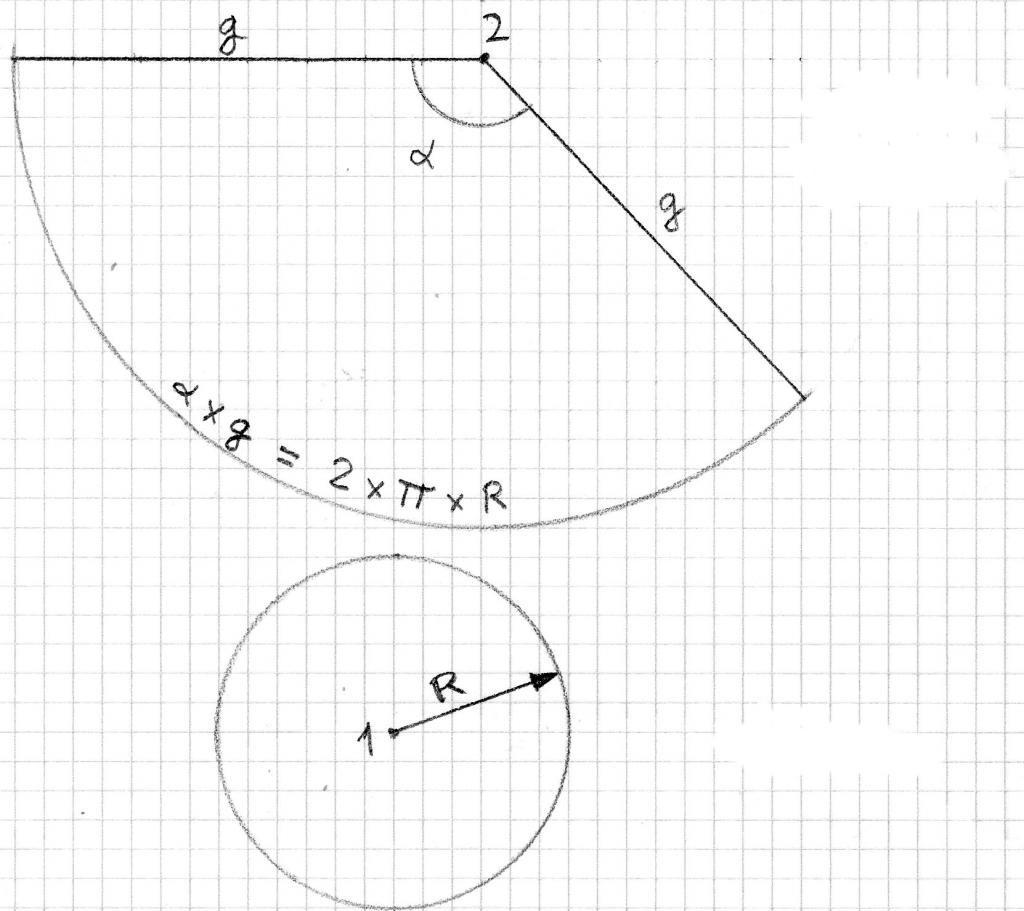
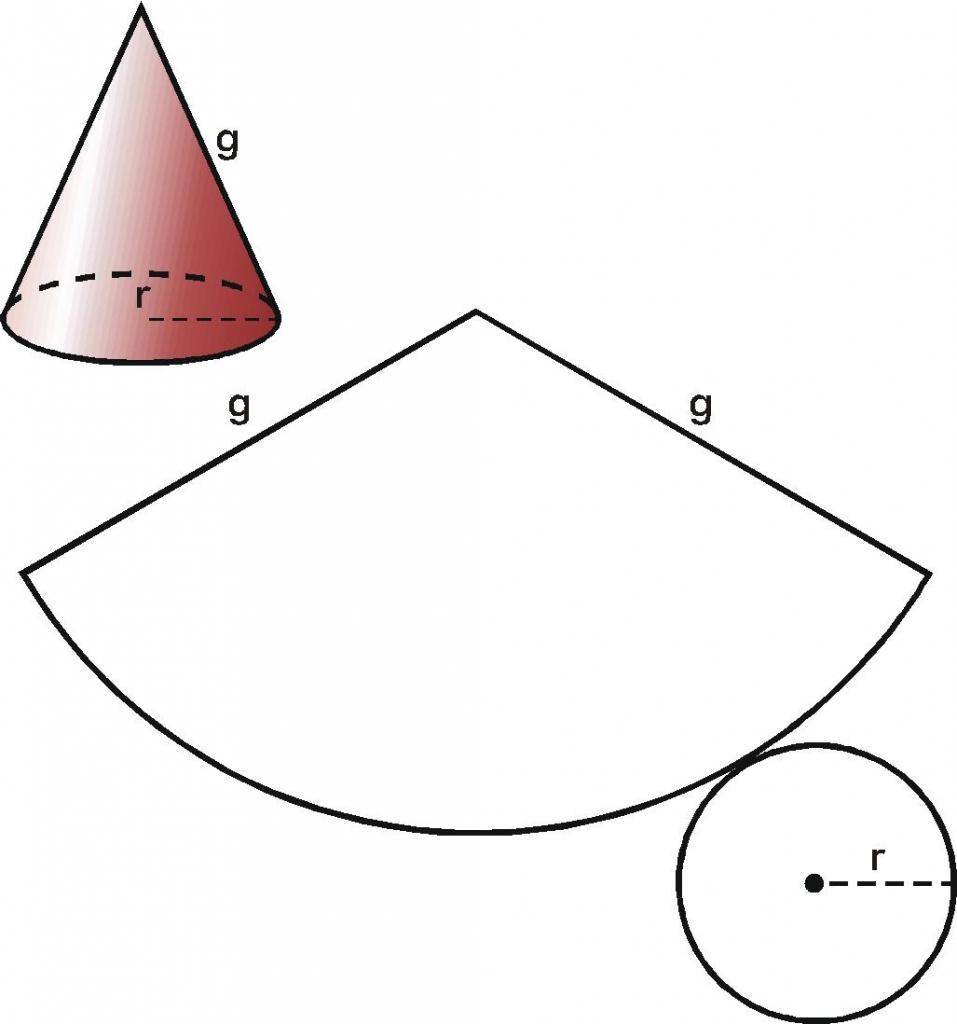
Как можно догадаться, конус образован двумя типами поверхностей. Одна из них - это плоский круг основания. Предположим, что он имеет радиус r. Вторая поверхность является боковой и называется конической. Пусть ее образующая будет равна g.
Если у нас имеется бумажный конус, то можно взять ножницы и отрезать от него основание. Затем, коническую поверхность следует разрезать вдоль любой образующей и развернуть ее на плоскости. Таким способом мы получили развертку боковой поверхности конуса. Две поверхности вместе с исходным конусом показаны на схеме ниже.
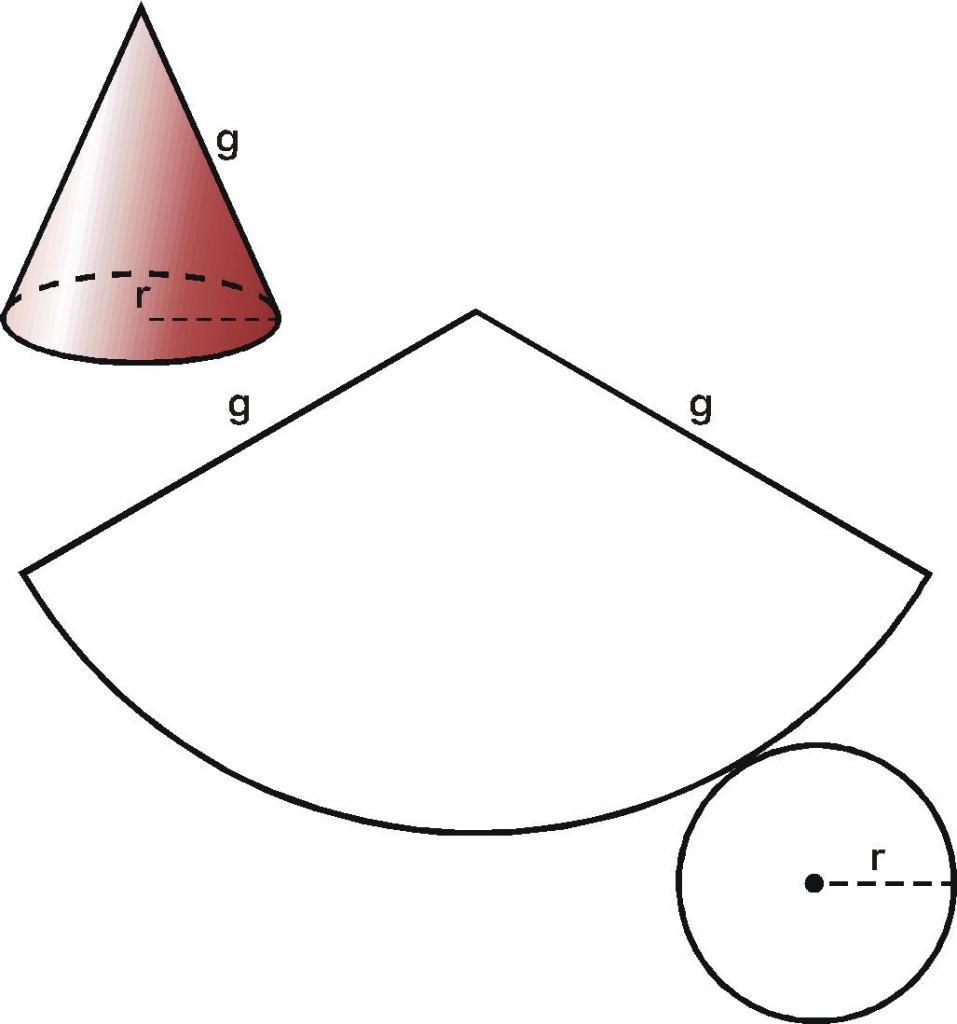
Внизу справа изображен круг основания. По центру показана развернутая коническая поверхность. Оказывается, что она соответствует некоторому круговому сектору круга, радиус которого равен длине образующей g.
Угол и площадь развертки
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.
Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:
Если бы весь круг радиусом g был построен, то его бы длина составила:
Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:
Тогда неизвестный угол φ будет равен:
Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:
Угол φ здесь выражен в радианах.
Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:
Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:
Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.
Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.
Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:
S = Sb + So = pi*r*(g + r).
Построение развертки конуса на бумаге
Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Пример решения геометрической задачи
Дан круглый прямой конус. Известно, что угол его боковой развертки равен 120o. Необходимо найти радиус и образующую этой фигуры, если известно, что высота h конуса равна 10 см.
Задача не является сложной, если вспомнить, что круглый конус - это фигура вращения прямоугольного треугольника. Из этого треугольника следует однозначная связь между высотой, радиусом и образующей. Запишем соответствующую формулу:
Вторым выражением, которое следует использовать при решении, является формула для угла φ:
Таким образом, мы имеем два уравнения, связывающих две неизвестные величины (r и g).
Выражаем из второй формулы g и подставляем результат в первую, получаем:
h2 + r2 = 4*pi2*r2/φ2 =>
Угол φ = 120o в радианах равен 2*pi/3. Подставляем это значение, получаем конечные формулы для r и g:
Остается подставить значение высоты и получить ответ на вопрос задачи: r ≈ 3,54 см, g ≈ 10,61 см.
1. Вычислите объём и площадь полной поверхности цилиндра, если его радиус R=5 cм, а длина образующей 11см.
2. Вычислите площадь осевого сечения, площадь полной поверхности и объём конуса, если его радиус равен 12см, а образующая 20см.
3. Площадь сферы равна 9π, найдите ее объём.
4. Найдите радиус шара, если расстояние от центра до плоскости сечения равно 12 см, а радиус сечения 9см.
5. Площадь осевого сечения цилиндра 56 см2, а площадь полной поверхности 88π см2. Найдите объем цилиндра.
6. Прямоугольный равнобедренный треугольник с катетом 5 см, вращается вокруг катета. Найдите площадь полной поверхности и объем получившегося тела.
7. Как относится площадь полной поверхности куба и вписанного в него шара?
Сделайте выводы, ответив на вопросы.
1) Почему цилиндр, конус и шар называют телами вращения?
2) Чем отличается шар от сферы?
3) Какой фигурой является осевое сечение цилиндра? Как находится площадь осевого сечения цилиндра, если известны радиус и высота цилиндра?
4) Какой фигурой является осевое сечение конуса? Как вычисляется площадь осевого сечения конуса, если известны радиус и высота конуса?
5) Какой формулой в конусе можно связать длину образующей (l), высоту(h) и радиус (R) ?
6) Площадь сферы вычисляется по формуле , выведите формулу для вычисления площади сферы через диаметр.
7) Приведите примеры реальных объектов, которые являются телами вращения. (например, корпус фломастера – это цилиндр) Приведите не менее трех примеров.
Как рассчитать площадь поверхности прямого кругового конуса по радиусу основания и образующей?
Площадь поверхности прямого кругового конуса равна сумме площадей основания конуса и боковой поверхности конуса.
Прямой круговой конус — конус в основании которого лежит круг и центр симметрии совпадает с центром этого круга (то есть это обычный, в простом понимании, конус).
Площадь основания конуса определяется по формуле:
Площадь боковой поверхности конуса, если известна длина образующей, определяется по формуле:
Полная площадь поверхности конуса равна:
Sп = Sо + Sб = Π*r 2 + П*r*l, где
h — высота конуса;
Π = 3.1415926535 — математическая постоянная, равная отношению длины окружности к её диаметру;
r — радиус основания конуса.
l — образующая конуса;
Длина образующей конуса равна минимальному расстоянию от вершины конуса до окружности основания конуса.
Полная площадь поверхности конуса равна сумме площадей основания конуса и боковой поверхности конуса.
Если радиус и высота конуса измерены в см (сантиметрах), то площадь конуса равна:
Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.
Вам будет интересно: Площадь основания правильной шестиугольной призмы. Формулы площади правильного шестиугольника
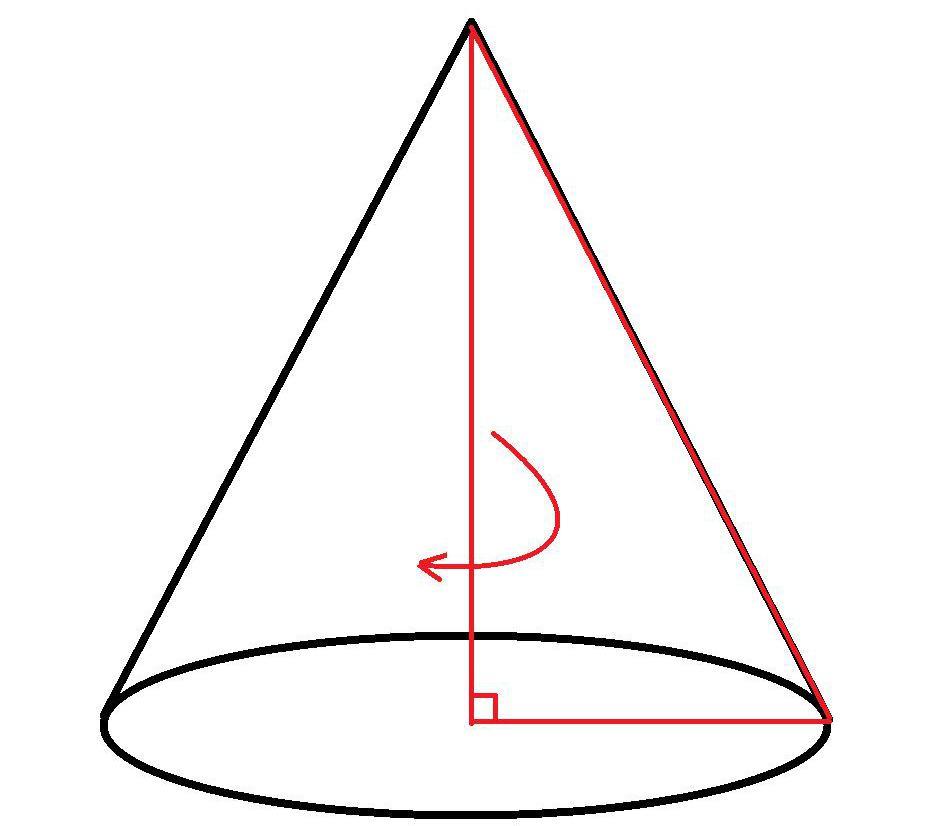
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.
Вам будет интересно: Жить - это не только существовать
Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.
Конус состоит из следующих элементов:
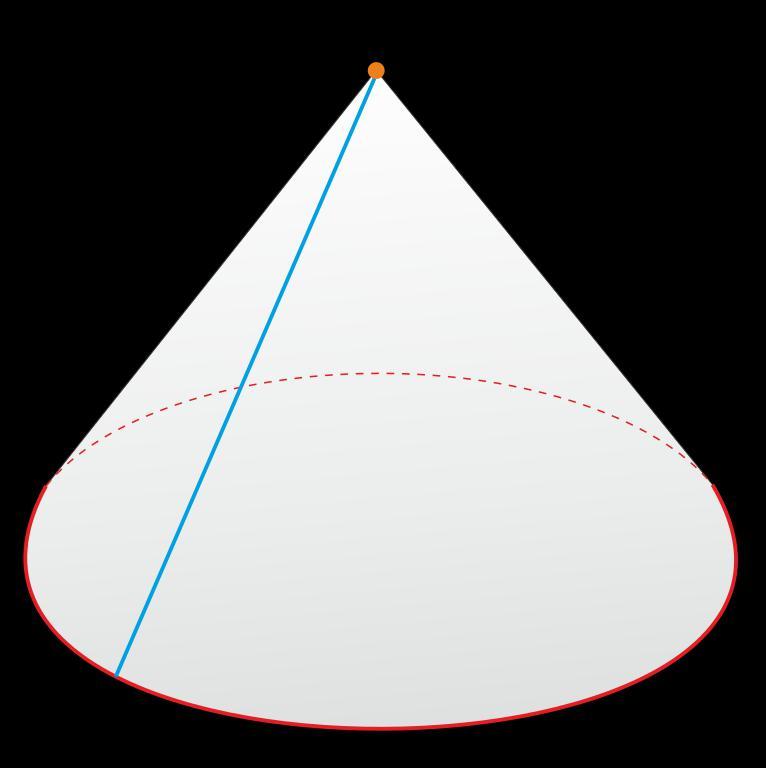
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.
Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.
Длина образующих в прямом конусе
Вам будет интересно: Значение выражения "угрюмый человек"
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.
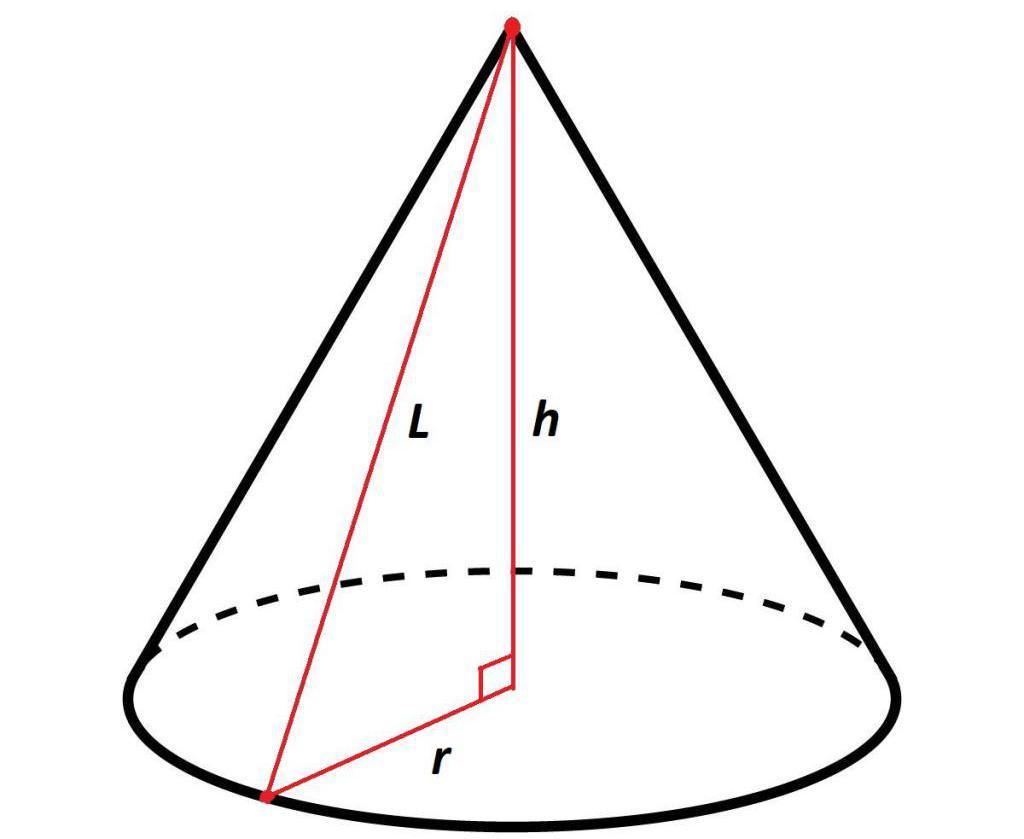
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l2 = r2+ h2 или l = √r2 + h2
где l – образующая;
Образующая в наклонном конусе
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.
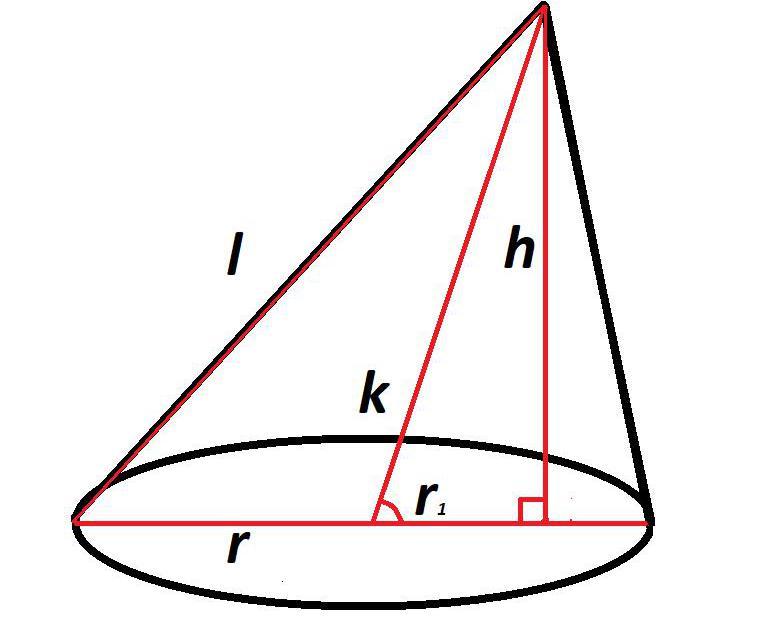
Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:
где r1 – это часть радиуса между осью и высотой;
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:
где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
r – радиус основания;
r1 – часть радиуса между осью и высотой.
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
или, не производя отдельно расчет R, объединить две формулы в одну:
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу - использованию теоремы Пифагора.
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
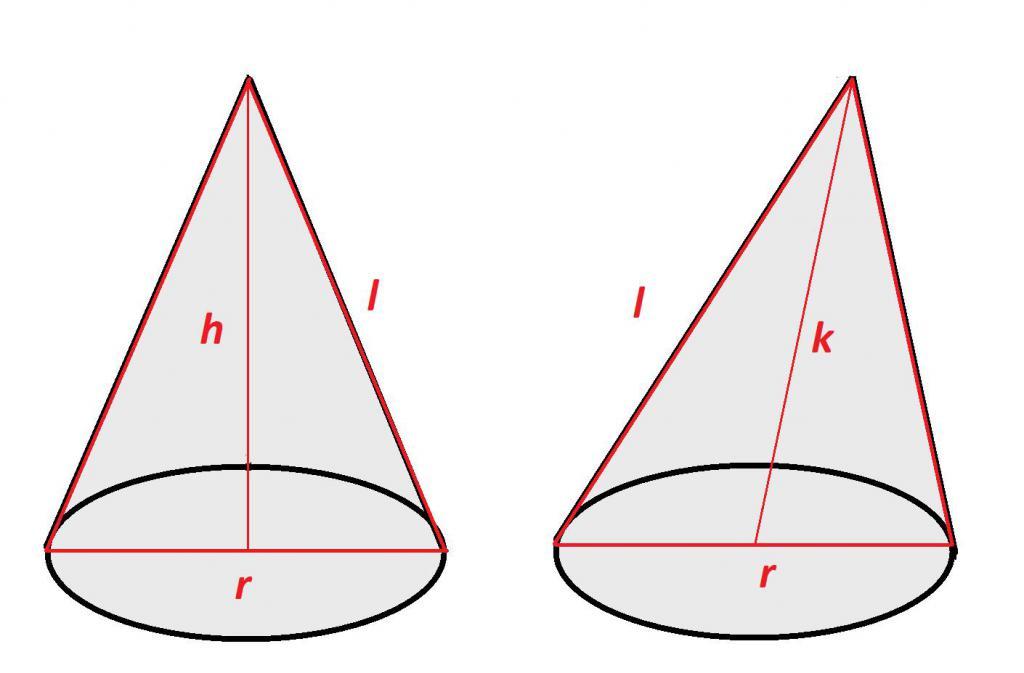
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие - оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где S – это площадь сечения;
d – диаметр основания;
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Расчет объема
Формула объема любого конуса выглядит следующим образом:
V = 1/3 * π * h * r2
где V – это объем конуса;
π - константа, равная 3,14.
Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Конус является объемной фигурой вращения, которая часто появляется в геометрических задачах. Как и всякая фигура, он обладает рядом линейных характеристик, площадью поверхности и объемом. В данной статье рассмотрим, что представляет собой конус, а также приведем формулу образующей конуса.
Конус в геометрии

Многие ели в жаркий летний день мороженое-рожок. Вафельный стаканчик этого мороженого имеет форму конуса. В геометрии более строгое определение этой фигуры следующее: конус представляет собой поверхность, которая получается в результате соединения с помощью прямых отрезков всех точек некоторой плоской кривой с фиксированной точкой пространства, не лежащей в плоскости упомянутой кривой. Если кривая является эллипсом, то конус будет эллиптическим, если окружностью - то круглым и так далее.
Вам будет интересно: Под сенью муз: художественная школа Мурманска
Данное выше геометрическое определение соответствует фигуре на рисунке ниже.
Здесь кривой, на которую опирается коническая поверхность, является окружность, центр которой лежит на вертикальной оси. Как видно из рисунка, хотя фигура является пространственной, но ее объем равен нулю. Если вместо окружности взять круг, тогда ограниченный этим кругом и конической поверхностью объем пространства будет объемом конуса.
Элементы фигуры
Перед тем как привести формулу образующей конуса, следует пояснить, из каких элементов состоит рассматриваемая пространственная фигура, и какие геометрические понятия используются для ее описания.
Ориентируясь на предыдущий рисунок, можно сказать, что конус образован двумя поверхностями:
- конической, которая называется также боковой;
- плоской фигурой (круг на рисунке), которая называется основанием конуса.
В отличие от полиэдров, конус не имеет граней и ребер, однако у него имеется одна единственная вершина, которая сверху ограничивает коническую поверхность. На предыдущем рисунке вершина находится в начале координат.
Для рассматриваемой фигуры также используют понятия образующей и направляющей. Что такое образующая конуса, и что такое его направляющая. Начнем с определения последней. Направляющей является кривая, ограничивающая основание фигуры. Названа она так, поскольку вдоль нее движется образующая, описывая коническую поверхность. Направляющая часто называется директрисой.
Образующая - это прямой отрезок, который соединяет вершину фигуры и любую точку направляющей. Образующих у конуса бесконечное множество. Их совокупность определяет коническую поверхность. Образующую также называют генератрисой.
Круглый прямой конус
Как отмечалось выше, основание конуса может быть ограничено любой плоской кривой. Тем не менее на практике и в геометрических задачах часто встречается круглый конус. Его и будем рассматривать далее в статье.
Круглый конус может быть прямым или наклонным. В первом случае перпендикуляр, проведенный из его вершины к основанию, пересекает последнее в центре круга. Прямой круглый конус является симметричной фигурой вращения, которую можно получить с помощью прямоугольного треугольника. Рисунок ниже показывает, как это делается.
На рисунке показан прямоугольный треугольник, который стоит на одном из своих катетов. Вокруг другого катета, являющегося осью, происходит вращение плоской фигуры. Во время вращения гипотенуза треугольника описывает коническую поверхность.
Линейные характеристики круглого прямого конуса
Ниже показан чертеж круглого конуса, на котором введены обозначения. Величина h - это высота фигуры, r - круглого основания радиус, который называется радиусом конуса, s - длина образующей.
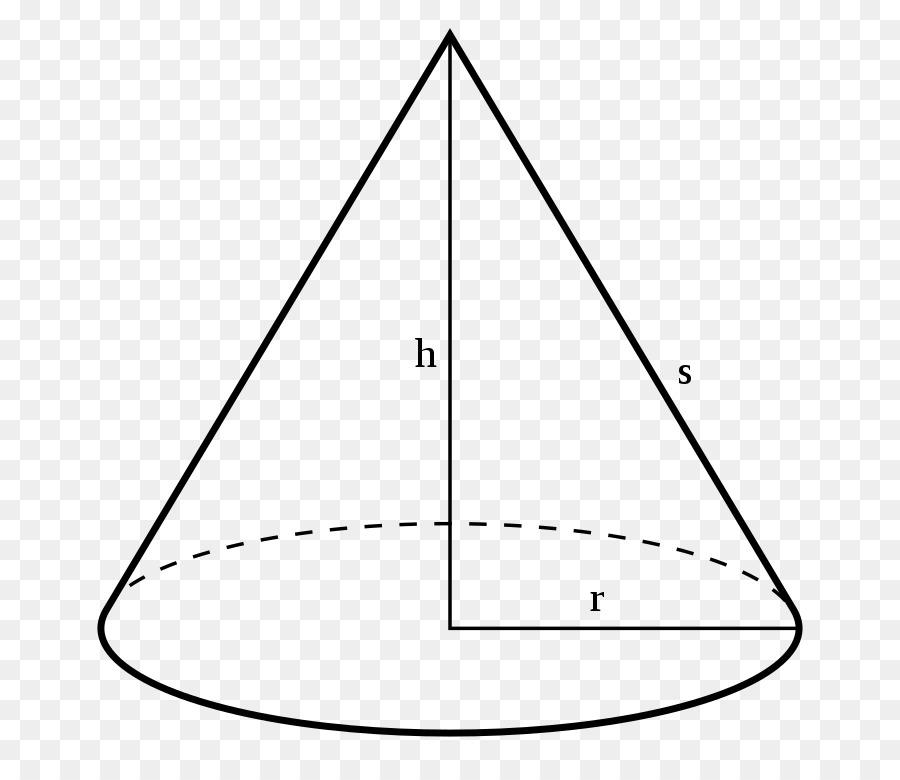
Очевидно, что все образующие s рассматриваемой фигуры имеют одинаковую длину. Это важное свойство присуще только прямому круглому конусу. Угол между любой образующей и осью вращения конуса является постоянной величиной при известных значениях r и h.
Как видим из рисунка, стороны r, h и s ограничивают прямоугольный треугольник. Этот факт позволяет применить теорему Пифагора для записи математического равенства, связывающего названные линейные характеристики конуса. Равенство имеет форму:
Это равенство содержит ответ на вопрос о том, как найти длину образующей конуса. Если известны радиус фигуры и ее высота, тогда:
Далее, на примерах решения задач покажем, как пользоваться формулой образующей конуса.
Задача с площадью конической поверхности и длиной окружности основания
Дан прямой конус с круглым основанием. Известно, что площадь его боковой поверхности равна 120 см2, а длина окружности основания составляет 30 см. Чему равна образующая конуса?
Решение этой задачи предполагает использование двух дополнительных формул, которые не были рассмотрены в статье. Приведем их ниже:
Первое выражение - это формула для вычисления площади конической поверхности Sb. Второе выражение знакомо каждому школьнику, это формула для определения длины окружности L.
Выражаем радиус r из второго выражения, подставляем его в первое:
Sb = pi × L / (2 × pi) × s
Тогда искомая формула длины образующей конуса примет вид:
Подставляем данные площади Sb и длины L в эту формулу, получаем ответ: s = 8 см.
Задача с площадью основания и высотой
Известно, что круглое основание конуса имеет площадь 40 см2. Высота фигуры в 2 раза больше диаметра этого основания. Необходимо найти длину генератрисы конуса.
Как и в предыдущем случае, запишем два уравнения, опираясь на условие задачи:
Первая формула - это известное выражение для площади круга. Второе равенство следует из того факта, что высота больше в 2 раза диаметра, а значит, в 4 раза радиуса r.
Читайте также: