Как зависит продольная температурная сила от длины закрепленной рельсовой плети

Обновлено: 04.05.2024

При проходе подвижного состава в плетях бесстыкового пути возникают значительные продольные силы, особенно на тормозных участках. Если не принять меры по предотвращению их отрицательного воздействия, то, суммируясь с температурными, они могут нарушить устойчивость пути. Следовательно, конструкция прикрепителей рельсовой плети к основанию должна не допустить разрушительного действия этих продольных сил угона.

К особенности бесстыкового пути следует отнести и специальные методы его восстановления. В процессе эксплуатации в рельсах возникают дефекты, недопустимые для безопасной эксплуатации пути, удаление которых связано с поэтапным выполнением ряда более сложных операций по сравнению со звеньевым путем.

Таким образом, бесстыковой путь, имеющий ряд бесспорных достоинств по сравнению со звеньевой конструкцией (комфортабельность пассажиров, меньшее сопротивлению движению, сокращение расходов на ремонты и содержание пути и подвижного состава и др.) имеет ряд особенностей в работе и определенные сложности при его содержании и восстановлении целостности лопнувших плетей. Поэтому конструкция бесстыкового пути должна быть повышенной надежности и долговечности для того, чтобы обеспечивать высокий уровень безопасности движения поездов.

Кроме общих требований к скреплениям, для бесстыкового пути особое значение имеет способность скреплений длительное время препятствовать продольным перемещениям плетей при движении поезда и температурных воздействиях. В большинстве стран применяется раздельное скрепление с жесткими и упругими клеммами. В Канаде, США, Австралии и некоторых других странах применяют костыльное скрепление с установкой пружинных противоугонов «в замок», как правило, по 4 шт. на каждой шпале. Такое решение в определенной мере обеспечивает совместный поворот шпалы и рельса при изгибе последнего во время прохода колес подвижного состава, что либо исключает местное проскальзывание подошвы рельса по подкладкам, либо резко его исключает. Для бесстыкового пути пригодны все виды подре6льсовых оснований: деревянные и железобетонные шпалы, рамы, плиты. При костыльном скреплении применяются только деревянные шпалы.

Температурные перемещения и силы

Построим объемлющую эпюру температурных сил в районе Гомеля. Рельсы Р65, R=20 т, r_л=6,5, r_з=25, Т=93˚.

Перепад температуры на преодоление стыкового сопротивления

Для оптимального интервала закрепления рельсовых плетей, равного для условий Беларуси от +25 до 35˚С, определим величину участка дыхания конца рельсовой плети для летних и зимних условий по формулам

Для нижней границы оптимального интервала закрепления

t_y=25˚C; =64,62м; =51,46м;

Для верхней границы - t_y=35˚C; =63,08м; =59,66м.

Изменение длины одного конца плети при повышении температуры после закрепления бесстыкового пути определяется по формуле:

Изменение длины плети при понижении температуры

Суммарные годовые перемещения конца рельсовой плети в первый год эксплуатации составят λ_г=λ₁+λ₂. При обратном ходе температур суммарные годовые температурные перемещения будут меньше указанных значений, т.к. при этом должно преодолеваться двойное стыковое сопротивление.

Проще пользоваться графо-аналитическим способом определения перемещения рельсовых плетей. Температурная работа рельсов, возникающая при изменениях температуры, проявляется или в виде температурных напряжений, или в виде температурных перемещений. При этом проявившиеся перемещения соответствуют непроявившимся напряжениям, а проявившиеся напряжения – непроявившимся перемещениям. В дальнейшем проявившиеся напряжения будем представлять в виде вертикально заштрихованной площади, а непроявившиеся напряжения, по которым можно определить перемещения рельса или конца рельсовой плети – в виде незаштрихованной площади, причем суммарная температурная работа (перемещения и напряжения, или только перемещения или только напряжения) всегда выражаются прямоугольником. На основании закона Гука получаем, что удлинение

Величина = представляет собой площадь эпюры состоявшихся температурных деформаций рельсов, т.е. прямоугольник высотой 25t и длиной 1. Площадь эпюры состоявшихся температурных деформаций рельсов (незаштрихованную часть эпюры напряжений) обозначим через S_λ, тогда λ= S_λ/E.

Указанная формула действительна не только для прямоугольной эпюры проявившихся перемещений, но и для любого очертания эпюры. Это в значительной степени облегчает определение фактических изменений длины лежащих в пути рельсов и плетей в любой интересующий нас момент, т.к. определение площади эпюры проявившихся перемещений рельсов графическим способом не представляет особого труда. Определить перемещения можно и по площади эпюры несостоявшихся температурных сил, которую в этом случае надо дополнительно разделить на площадь поперечного сечения рельса.

4.7 Влияние стыкового сопротивления

Влияние стыкового сопротивления на температурную работу (напряжения и перемещения) рельсовых плетей бесстыкового пути хорошо видно из объемлющей эпюры температурных сил. С увеличением стыкового сопротивления уменьшается площадь проявившихся температурных перемещения, что естественно приводит к уменьшению температурных деформаций и участков дыхания конца рельсовой плети. При этом облегчается температурная работа уравнительного пролета, а меньшие величины стыковых зазоров снижают уровень взаимодействия пути и подвижного состава и продлят срок их службы. Кроме восьмидырных накладок, хорошо зарекомендовавших себя в процессе эксплуатации, на ряде железных дорог пытались применять в уравнительном пролете 12-дырные накладки. Для согласованной работы стыков уравнительного пролета в первом стыке от плети устанавливают восьмидырные, а во втором – шестидырные накладки. При одинаковом стыковом сопротивлении в основном работает первый стык от плети.

Длина участка «дыхания» конца рельсовой плети в момент наступления максимальной расчетной температуры определяется по формуле

1Нелюбов А.И., Новад А.А. Динамика полета боевых летательных аппаратов. ВВИА им. Н.Е. Жуковского, 1992 . 439с.

1.1 Факторы, влияющие на температуру рельсов.

Изменение температуры рельса происходит в условиях сложного теплообмена.

Летом, находясь под действием солнечных лучей, рельсы получают тепловую энергию, тратя её часть на обратное излучение и теплоотдачу в окружающую среду. Когда рельс нагревается(тепла подводится больше, чем отводится), значения температуры в разных его точках, изменяясь во времени, всё больше возрастают.

При достижения равновесия (теплового) между количеством подводимого и отдаваемого тепла температура рельсов перестаёт повышаться, хотя локальные значения температуры различных участков как по длине рельса, так и по его поперечному сечению могут довольно существенно различаться. Наблюдаемая разница в температуре по поперечному сечению рельса (головка, шейка, подошва)достигает 10ºС. Затем температура рельса понижается, а его температурное поле выравнивается.

Температура рельсов зависит от многих факторов: температуры воздуха, типа рельса и состояния его поверхностей, а также ориентирования рельса относительно сторон света, плана и профиля пути; поперечного профиля земляного полотна (насыпь, выемка, нулевое место), интенсивности солнечной радиации и прозрачности атмосферы, скорости и направления ветра, качества и отражательной способности балласта и ряда других причин.

При одной и той же температуре воздуха и различных сочетаниях других перечисленных факторов отличие температур в зависимости от условий может достигать 10º-15ºС и даже более.

Температура рельсов летом в дневные часы, как правило, выше температуры рельсов. Разница температур рельса и воздуха является величиной переменной и с повышением максимальной температуры воздуха несколько уменьшается. Разница температур рельса и воздуха летом достигает 16-18ºС в северных регионах и 24-26ºС- в средних и южных районах страны. За расчётную разницу температур между ними летом в настоящее время принимают 20ºС, т.е.

где tр- температура рельса;

tв- температура воздуха.

Зимой температура рельсов меньше отличается от температуры воздуха. Наблюдения показали, что в зоне экстремальных зимних температур воздуха ( -30ºС и ниже) их температура может быть на 3-5ºС выше по сравнению с воздухом. Из-за выхолаживания при сильном ветре температура может быть и ниже температуры воздуха. Однако обычно зимой температура рельсов и воздуха совпадает, и в расчётах принимают tр = tв.

При изготовлении и укладки рельсовых плетей, производстве работ по техническому обслуживанию и ремонту бесстыкового пути измеряют фактическую температуру рельсов. В настоящее время таковой принято считать температуру головки рельса. При подобных измерениях применяют различные технические средства: приборы для непосредственного измерения в пути на месте производства работ; стационарные приборы для измерения на постах метрологических станций и дистанции пути; стационарные или переносные приборы для измерения на рельсосварочных предприятиях в процессе изготовления плетей. Впервые температура рельсовой плети измеряется на рельсосварочном предприятии, где определяется та, при которой изготовлена плеть.

В проекте укладки бесстыкового пути каждой паре рельсовых плетей присваивается порядковый номер, под котором в дальнейшем она будет значиться в заявке на сварку и других учётных документах.

В начале и конце каждой плети на внутренней стороне шейки рельса (со стороны оси пути) белой масляной краской указывается номер рельсосварочного предприятия, номер плети по сварочной ведомости, её длина в метрах с точностью до второго знака после запятой при температуре рельсов +20ºС. При иной температуре рельсовая плеть, очевидно, будет иметь другую длину. Изменение ∆L длины рельсовой плети в этом случае может быть определено по формуле

∆L = 0.0000118L (20 – t _ф), (1.1)

где L - длина рельсовой плети при температуре +20ºС (указана на внутренней стороне шейки рельса);

t _ф - температура рельсовой плети в момент измерения.

Пример 1.1. Длина рельсовой плети, изготовленной, на предприятии 42 по сварочной ведомости 317, составляет 796,22 м, а температура рельса 18ºС. Какую длину плети следует указать на внутренней стороне шейки рельса?

Изменение длины рельсовой плети составит

На внутренней стороне шейки рельса должна быть указана длина

Допустим, что номер плети по проекту 12, плеть правая. Она уложена в путь 12 июня 2004 г. при температуре закрепления tо=+24ºС. Тогда маркировка такой плети имеет вид:

После укладки рельсовой плети в путь дополнительно к имеющейся маркировке наносят номер плети по проекту с указанием сторонности (левая по ходу км – Л, правая по ходу км - П), дату укладки и температуру плети при закреплении её к основанию (шпалам).

При закреплении плетей на шпалах температуру рельсов измеряют дважды- перед началом и после окончания закрепления. Для ускорения процесса измерения температуры рельсовых плетей сначала их закрепляют только на каждой пятой шпале.

С момента закрепления рельсовой плети на постоянный режим начинается «температурная жизнь» плети, а сама температура закрепления может считаться началом этой жизни. Температуру закрепления рельсовой плети иногда называют «нейтральной».

1.2 Изменение длины рельсов при колебаниях их температуры.

Если положить рельс длиной L на ролики или специальные подкладки с очень низким коэффициентом трения, то можно считать, что свободному удлинению рельса ничто ни препятствует.

Изменение длины рельса ∆L, как свободного стержня, при изменении его температуры может быть определено по формуле

где α - коэффициент линейного расширения рельсовой стали;

α = 0,00001181/град; ∆t р- изменение температуры рельса,ºС,

L - длина рельса, м.

Пример 1.2.На специальные подкладки с очень низким коэффициентом трения положили рельс длиной 985,50 м при температуре 28ºС. Температура рельса повысилась до 35ºС. Насколько изменилась длина рельса?

где α- коэффициент линейного расширения рельсовой стали;

α=0,00001181/град;

∆t р- изменение температуры рельса,ºС,

L- длина рельса, м.

∆L=0,0000118∙985,5∙(35-28)=0,08 м.

Таким образом, при изменении температуры свободно лежащего рельса длиной 985,50 м на 7º С его длина увеличилась на 80 мм. В этом случае ничто не препятствовало этому изменению и напряженное состояние рельса не возникло.

Однако в пути рельс лежит на металлических подкладках, прикреплён к каждой шпале мощным промежуточным скреплением, а с соседним рельсом соединён стыковым скреплением, поэтому изменение длины рельса в реальных условиях не может происходить так свободно. Изменение длины рельсовой плети в зависимости от температуры описывается более сложным законом, учитывающим преодоление погонных и стыковых сопротивлений.

Рассмотрим другой крайний случай. Допустим, что рельс жестко закреплён по концам и вообще его длина постоянна.

Изменение температуры рельса, которое не может повлиять на его длину, вызывает в нём температурные напряжения, а они согласно закону Гука пропорциональны величине несостоявшегося температурного удлинения (укорочения) рельса и противоположны ему по знаку. Другими словами, если рельс при повышении его температуры не смог удлиниться, то в нём возникли температурные напряжения сжатия; если рельс при понижении его температуры не смог укоротиться, то в нём возникли температурные напряжения растяжения.

Температурные напряжения, возникающие в рельсе, если его длина сохраняется при изменении температуры относительно нейтральной, могут быть определены по формуле

σ _t = E ∆L / L = α E ∆tр, (1.3)

где E- модуль упругости рельсовой стали, E - 2,1∙10 кг/см 2 = 21∙10 МПа;

∆L/L- несостоявшееся относительное удлинение рельса.

Продольная температурная сила, сжимающая или растягивающая (в зависимости от направления изменения его температуры) рельс, может быть определена по формуле

Работы по введению плетей в расчетный температурный интервал с использованием гидравлического натяжного устройства (ГНУ) типа ТН-70, СНП-80-500 или других выполняются при температуре рельсов ниже расчетной температуры закрепления.

Перед началом работы должны быть выполнены расчеты по определению изменений длин плети ΔL и прилагаемого растягивающего усилия P, необходимого для удлинения плети (или полуплети). Удлинение плети ΔL определяется по формуле:

где L – длина плети, м;

t_з – расчетная температура рельсов при закреплении плети на постоянный режим работы (устанавливается дистанцией пути в зависимости от ее региональности, в соответствии с Техническими указаниями по устройству, укладке, содержанию и ремонту бесстыкового пути), ºС;

t_у – температура рельсовой плети в момент ее первоначальной укладки, ºС;

α=0,0000118 – коэффициент температурного расширения рельсовой стали.

А растягивающее усилие определяется по формуле:

где E – модуль упругости рельсовой стали (E=2,1·10 7 Н/см 2 );

F – площадь поперечного сечения рельса типа Р65 (F=82,65 см 2 );

Δt – разница между ожидаемой на время «окна» и расчетной температурой плети при закреплении ее на постоянный режим работы.

Для обеспечения неподвижности уравнительных рельсов с обеих сторон от удлиняемой плети должны находиться анкерные участки. Рельсовые стыки, расположенные в пределах анкерных участков и прилегающие к ним, должны обеспечивать нормативное стыковое сопротивление продольному перемещению рельсов R (для рельсов типа Р65 R=400кН), что достигается затяжкой гаек стыковых болтов крутящим моментом, равным 600 кН·м.

Длина анкерного участка, м, со стороны «подвижного» конца плети определяется по формуле:

где r=25 кН/м – погонное сопротивление рельсов продольному перемещению.

Для обеспечения значения r=25 кН/м необходимо, чтобы гайки клеммных и закладных болтов на уравнительных рельсах со стороны подвижного конца рельсовой плети ( в месте установки ГНУ) на длине анкерного участка имели усиленную затяжку (М=220÷240 Н·м).

Длина и место расположения анкерного участка со стороны неподвижного конца рельсовой плети определяется исходя из следующих условий:

1) если P_R_н=400 кН, то гайки клеммных и закладных болтов подтягиваются на уравнительных рельсах со стороны неподвижного конца плети до значения М=220 Н·м на длине

2) если Р≥R_н=400 кН, то закрепляется неподвижный конец самой рельсовой плети (М=220 Н·м) на длине

и прилегающие к нему уравнительные рельсы на длине

Для контроля равномерности удлинения плети на подошву рельса в створе с краем подкладки через каждые 50 м наносят риски, расчетное перемещение которых

где а_i – расстояние от неподвижного конца плети до i-й риски (50,100, 150 м и т.д.).

В подготовительный период выполняют следующие работы:

- определяют расчетное удлинение плети ΔL и в соответствии с ним заготавливают укороченный уравнительный рельс (рельсы);

- завозят укороченный уравнительный рельс на место работ;

- производят регулировку зазоров соответственно температуре рельсов;

- исходя из ожидаемой температуры рельсов в день «окна» вычисляют по формулам (2) – (7) остальные необходимые параметры.

В день производства работ до «окна»:

- закрепляют анкерный участок со стороны неподвижного конца плети;

- наносят риски через 50 м;

- после ограничения скорости до 25 км/ч на каждой 15-й шпале устанавливают подвесные ролики (рис. 9.1).

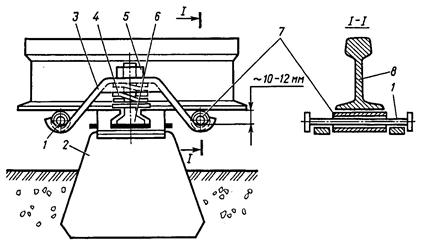
Рис. 9.1. Подвесные ролики для разрядки напряжений в плетях без перерыва движения поездов: 1 – ось ролика; 2 – железобетонная шпала; 3 – коромысло; 4 – дополнительная двухвитковая шайба; 5 – гайка; 6 – клеммный болт; 7 – трубка ролика; 8 - рельс

- заменяют уравнительный рельс со стороны удлиняемого конца плети на укороченный, закрепляют анкерный участок;

- ослабляют гайки клеммных болтов, вывешивают плеть и встряхивают ее ударами деревянных кувалд. Полноту разрядки оценивают по общему укорочению плети

Δ l = L (t _у – t _p) α , где t _p – температура рельсов в данный момент. Равномерность разрядки оценивают по смещению рисок, которое определяется по формуле:

_I = α a _I (t _y – t _p ), где а _i – расстояние от неподвижного конца плети до i-й риски (50, 100, 150 м).

- наносят новые риски на подошве рельса через каждые 50 м на расстоянии от края подкладок, определяемому по формуле (9.7);

- производят растяжение плети. В процессе растяжения плети при необходимости (особенно в кривых участках) ее встряхивают ударами деревянных кувалд или механическими вибраторами. Когда зазор между плетью и укороченным рельсом сократится до необходимого значения, растяжение прекращают. Правильность выполнения работ контролируется по трем критериям: полному расчетному удлинению плети; соответствию расчетного усилия Р [формула 9.2] приложенному (по отсчету на приборе); расчетному смещению каждой из рисок (риски должны совпадать с краями подкладок);

- перед демонтажем ГНУ закрепляют на шпалах «подвижный» конец плети (М=220 Н · м) на длине λ₄ = P / r;

- ставят накладки и сболчивают стык между плетью и укороченным рельсом;

- закрепляют плеть на каждой шестой шпале и открывают движение поездов со скоростью 25 км/ч;

- после окончательного закрепления плети на всех шпалах отменяют предупреждение об уменьшении скорости движения поездов.

Пример расчета параметров для принудительного ввода плетей в расчетный интервал температур. Исходные данные: плеть длиной L=800 м; рельсы типа Р65; температура рельсов в момент первоначальной укладки плети t_y = +5 ºC; ожидаемая температура рельсов на день «окна» t_p = -3 ºС; расчетный температурный интервал закрепления – от +18 до +25ºС, принимаем t_з = +25 ºС; Δt = 22-(-3) = 25 ºС.

Используя формулы (9.1) – (9.7), выполним следующие вычисления.

1. Изменение длины плети при введение ее в расчетный интервал закрепления (рис. 9.2)

ΔL = L(t _з – t _y ) α = 800(22-5)0,0000118 = 0,160 м = 160 мм.

2. Усилие, необходимое для удлинения плети

Р = α E F Δ t = 11,8·10 -6 ·2,1·10 7 ·82,65·25 = 512 кН.

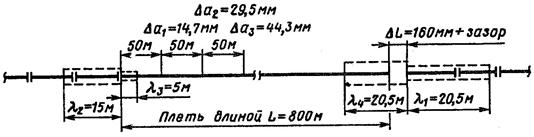
Рис. 9.2. Схематическое изображение расчетных параметров при принудительном (с применением гидравлических натяжных устройств) вводе рельсовых плетей в расчетный температурный интервал

3. Укорочение плети после ее раскрепления

Δl = L(t _y – t _p) α = 800[5-(-3)]11,8·10 -6 = 0,076 м = 76 мм.

4. Смещение рисок при укорочении плети после ее раскрепления: первая риска через 50 м от неподвижного конца плети

вторая риска

Δl₂ = 11,8·10 -6 ·100·8 = 0,0094 м = 9,4 мм;

третья риска

Δl₃ = 11,8·10 -6 ·150·8 = 0,0141 м = 14,1 мм.

5. Размеры анкерных участков:

со стороны подвижного конца плети

λ₁ = P/r = 512/25 = 20,5 м;

со стороны неподвижного конца плети: так как P>R_н, следовательно

подвижный конец плети после удлинения, требующий срочного закрепления

4.ИССЛЕДОВАНИЯ ТЕМПЕРАТУРНОЙ РАБОТЫ КОНЦЕВЫХ УЧАСТКОВ РЕЛЬСОВЫХ ПЛЕТЕЙ БЕССТЫКОВОГО ПУТИ

В настоящее время достаточно полно разработана теория температурных деформаций длинных рельсов . При расчетах температурных перемещений концов рельсовых плетей бесстыкового пути пользуются формулами и приемами, заимствованными из теории длинных рельсов. Однако не во всех случаях эти формулы и приемы пригодны.

Длинный рельс в отличие от бесстыковой плети при годовом цикле колебаний температуры всей своей длиной участвует в активной работе, т. е. сопротивление продольным перемещениям рельса преодолевается по всей его длине. Если сопротивление равномерно распределено по всей длине рельса, то длина активного участка с каждого конца рельса равна половине длины этого рельса. В бесстыковом пути в активной температурной работе принимают участие только концевые части плети. Средняя часть работает как жестко заделанный стержень. Протяженность активного участка непостоянна и зависит от ряда факторов. Это в значительной степени усложняет расчет бесстыкового пути по сравнению с расчетом длинных рельсов. Тем не менее совершенно необходимо производить расчеты температурных перемещений концевых участков бесстыковых рельсовых плетей и возникающих в этих участках напряжений.

Расчеты необходимы для выбора способов стыкования рельсовых плетей. Кроме того, на концевых участках в зоне активной температурной работы рельсовых плетей, как будет показано ниже, при некоторых условиях возможно появление напряжений, превышающих максимальные расчетные напряжения в средней части плети. Так как это явление весьма нежелательно, необходимо знать, при каких условиях оно возможно и как его избежать, К сожалению, до последнего времени не было возможности проанализировать полный годовой цикл температурной работы рельсовой плети.

Наиболее полные расчетные формулы, данные проф. Г. М. Шахунянцем тюзволяют определить удлинение рельсовой плети от момента ее укладки до наступления максимальной температуры и от момента укладки до минимальной температуры с учетом увеличения погонного сопротивления при смерзании балласта. Однако при помощи этих формул нельзя проанализировать температурную работу концевых участков рельсовых плетей при изменении их температуры от минимума до максимума с учетом понижения погонного сопротивления при оттаивании балласта. Следовательно, нельзя построить диаграмму стыковых зазоров при эксплуатации пути и проанализировать температурные напряжения, возникающие в зоне активной температурной работы.

4.1 Сопротивление продольным деформациям

В условиях эксплуатации железнодорожного пути имеются стыковое и рассредоточенное погонное сопротивления.

Стыковое сопротивление обусловлено в основном силами трения между подвижными и неподвижными элементами стыкового соединения. При наличии болтовых стыков — это силы трения между рельсом и стыковыми накладками. После того как стыковой зазор увеличится до конструктивных размеров, дальнейшему сокращению плети и увеличению зазора сопротивляются стыковые болты, которые в этом случае включаются в работу на изгиб. В том случае, когда стыковой зазор равен нулю, при дальнейшем увеличении длины плети возникает торцовое давление рельсовых плетей друг на Друга.

В болтовых стыках можно использовать все три вида сопротивления, т. е. силы трения между рельсом и накладками, торцовое давление рельсов и сопротивление болтов изгибу. Однако использовать сопротивление болтов изгибу нерационально, а по использованию торцового давления необходимо провести дополнительные исследования, так как возникает опасность откола головки рельсов.

В уравнительных приборах обычно используются только силы трения. Величины их, как правило, невелики, и в расчетах температурных деформаций ими можно пренебречь.

Силы трения металла по металлу мало зависят от сезонных изменений температуры. Поэтому в дальнейших расчетах стыковое сопротивление Rс принимается постоянной величиной, не зависящей от величины перемещения и от температуры.

Погонные сопротивления проявляются значительно сложнее. Наблюдения показали, что в летний период при незамерзшем балласте и раздельных промежуточных скреплениях перемещение рельса вызывает перемещение шпал в балласте. В этот период погонные сопротивления определяются сопротивлением балласта перемещению шпал вдоль пути. Сопротивление балласта частично упруго и до некоторых пределов зависит от величины перемещения. Зимой, когда балласт смерзается, сопротивление его резко возрастает и становится больше сопротивления перемещению рельсов по шпалам. В этом случае шпалы остаются практически неподвижными, а рельс перемещается относительно шпал. Погонное сопротивление при замерзшем балласте определяется силами трения между рельсом и скреплением, является величиной неупругой и теоретически не зависит от величины перемещения.

При оценке сопротивляемости балласта обычно пользуются экспериментальными данными, полученными при смещении одной или нескольких шпал. Однако следует иметь в виду, что смещение шпал при опыте производится на значительную величину поступательно за короткий промежуток времени и без периодического воздействия поездов. В эксплуатационных же условиях имеет место возвратно-поступательные смещения, которые происходят в течение длительного времени при частом воздействии нагрузки от проходящих поездов. Поэтому без доказательств нельзя утверждать, что выявленная при разовом смещении шпаты закономерность р = /(А) сохранится в эксплуатационных условиях и будет пригодна для определения годовых температурных перемещений конца рельсовой плети. Автором сделана попытка определить погонное сопротивление, проявляющееся в процессе эксплуатации пути. Работа эта в настоящее время еще не закончена, однако некоторые результаты уже получены.

При исследованиях велись записи температурных перемещений концов рельсовых плетей и колебаний температуры рельсов. Перемещения записывались с десятикратным увеличением. Опыты проводились на плетях из рельсов типа Р50 с раздельными скреплениями по типу марки К, на деревянных шпалах и щебеночном балласте. Приборы были установлены на четырех концах рельсовых плетей, соединенных друг с другом уравнительными рельсами и шестидырными болтовыми стыками типовой конструкции.

В летний период при незамерзшем балласте получены записи перемещений концов рельсовых плетей при прямом ходе изменения температуры и при обратном ходе на ту же величину.

Самопишущими приборами зафиксировано весьма любопытное, явление. При проходе поездов концы рельсовых плетей перемещаются вдоль пути. В тех случаях, когда температура, достигнув некоторой величины, остается постоянной, температурные силы в рельсовой плети уравновешиваются сопротивлением балласта и дальнейшего изменения длины плети не происходит, продольные перемещения концов плети под поездом имеют упругий характер, т. е. после прохода поезда эти перемещения полностью ликвидируются. Величина упругих перемещений, как показали наблюдения, в некоторых пределах зависит от величины продольных сил в рельсе и составляет 1—2 лш. Направление упругих перемещений конца рельсовой плети под поездом зависит от того, какие напряжения в рельсовой плети имеются: сжимающие или растягивающие.

В тех случаях, когда температура понижена по сравнению с температурой закрепления плети и рельсовая плеть стремится сократить свою длину, а балласт препятствует этому, при проходе поезда происходят перемещения в сторону удлинения плети. При обратном положении, когда температура выше температуры закрепления плети, проход поездов вызывает упругие перемещения концов в сторон>' сокращения длины плети. Например, в жаркую погоду летом, когда рельсовая плеть стремится удлиниться, при проходе поезда принимающий конец ее перемещается в сторону движения поезда (создается положение, похожее на угон), а отдающий конец перемещается в сторону, противоположную движению поезда (это уже мало похоже на угон). Оба конца плети перемещаются в направлении к ее середине. Осенью, когда рельсовая плеть стремится сократить свою длину, происходит обратное явление: оба конца перемещаются в направлении от середины плети. Проход поездов не только не уменьшает сопротивляемость балласта, а наоборот, как бы временно увеличивает его. Очевидно, этим можно объяснить способность балласта длительное время сопротивляться температурным силам в рельсе, несмотря на сложные условия работы пути. Следовательно, это явление весьма благоприятно для бесстыкового пути и его нужно внимательно изучить. Очевидно, оно оказывает существенное влияние на закономерности проявления угона пути и на работу противоугонов. С этой точки зрения указанное явление также заслуживает внимания. Таким образом, летнее сопротивление продольному перемещению рельсов, определяемое сопротивлением балласта, представляет собой довольно сложное явление, в котором еще не все изучено.

В дальнейшем, исследуя температурную работу рельсовых плетей в годовом цикле колебаний температуры, будем принимать все виды сопротивлений (стыковое сопротивление, погонное сопротивление зимой и летом) величинами постоянными, неупругими и не зависящими от величины перемещения.

4.2 Методы расчета продольных температурных перемещений и напряжений в рельсовых плетях бесстыкового пути

Существует графический и аналитический способы расчета продольных температурных перемещений и напряжений в рельсовых плетях бесстыкового пути. Графический метод расчета базируется на построении эпюры продольных сил в рельсовой плети. Эпюрой продольных сил называется график, показывающий величину продольной силы в каждом сечении рельсовой плети. По горизонтали откладывается длина рельсовой плети или того участка плети, для которого строится эпюра сил. По вертикали откладывается величина продольной силы. График строится в определенном масштабе.

В каждом сечении рельсовой плети продольная температурная сила не может быть больше суммы сил сопротивления продольному перемещению на участке от рассматриваемого сечения до конца плети. Помня это правило и зная имеющиеся сопротивления, легко построить эпюру возможных максимальных продольных сил в рельсовой плети.

При наличии стыкового сопротивления Re и погонного сопротивления р максимальная продольная сила в каждом сечении определяется уравнением

Nmax=Rc+pl,

где l — расстояние от рассмотренного сечения до конца плети.

Эпюры продольных сил или напряжений строят в такой последовательности: 1) при максимальной температуре; 2) при понижении температуры до температуры смерзания балласта; 3) при минимальной температуре; 4) при г повышении температуры до температуры оттаивания балласта; 5) при у максимальной температуре.

Построения эпюры будем производить для следующих условии:

-температура закрепления рельсовой плети типа Р65 ty = +25> С;

-максимальная температура t_max= -С56°С;

-минимальнаятемпература t_min =-37°С;

-стыковое сопротивление Rc = 20 000 кГ;

-погонное сопротивление по одной нити р = 6,5 кГ см;

Рассмотрим последовательное изменение продольных сил при изменении температуры и построим эпюры. Максимальные температурные силы в зоне пассивной температурной работы пропорциональны приращению температуры и определяются уравнением

N=aEF ∙Δt.

В зоне активной температурной работы на концевом участке максимальные продольные силы равны силам сопротивления продольному перемещению. При многократных взаимообратных изменениях температуры на разную величину эпюра продольных сил в зоне активной температурной работы может быть довольно сложной.

Допустим, что после укладки и закрепления рельсовой плети температура поднялась до некоторого максимального значения /W, при наличии стыкового сопротивления Rc и погонного сопротивления р эпюра продольных сил при tmax будет такой, как показано на рисунке (эпюра 2), перемещение конца рельсовой плети определим по формуле:

Затем предположим что температура начинает понижаться. Когда температура рельса понизится до той температуры, при которой рельс был закреплен, в зоне пассивной температурной работы, т. е. в средней части плети, продольные температурные силы будут равны нулю (эпюра 3).

При дальнейшем понижении температуры, когда будет преодолено стыковое сопротивление, конец плети начнет перемещаться к середине плети, т. е. длина плети начнет уменьшаться, перемещение можно рассчитать по формуле:

где t₀ - температура смерзания балласта.

Далее рассчитаем перемещение при достижении минимальной температуры по формуле :

Читайте также: